Глубокое обучение объяснили моей 8-летней дочери
Машинное обучение и особенно глубокое обучение — горячие темы, и вы наверняка встречали модное слово «искусственный интеллект» в СМИ.

Однако это не новые концепции. Первая искусственная нейронная сеть (ИНС) была представлена в 40-х годах. Так почему же в последнее время такой интерес к нейронным сетям и глубокому обучению?
Мы рассмотрим эту и другие концепции в серии сообщений блога о графических процессорах и машинном обучении .
Я помню, как в 80-е мой отец создавал распознавание символов для банковских чеков. Он использовал примитивы и производные для определения уровня темноты пикселей. Изучение стольких разных типов почерка было настоящей болью, потому что ему требовалось одно уравнение, применимое ко всем вариантам.
В последние несколько лет стало ясно, что лучший способ справиться с подобными проблемами — это сверточные нейронные сети. Уравнения, разработанные людьми, больше не подходят для обработки бесконечных почерков.
Давайте рассмотрим один из самых классических примеров: построение системы распознавания чисел, нейронной сети для распознавания рукописных цифр.
Мы начнем с подсчета, сколько раз маленькие красные фигурки в верхнем ряду можно увидеть на каждой из черных рукописных цифр (в левом столбце).
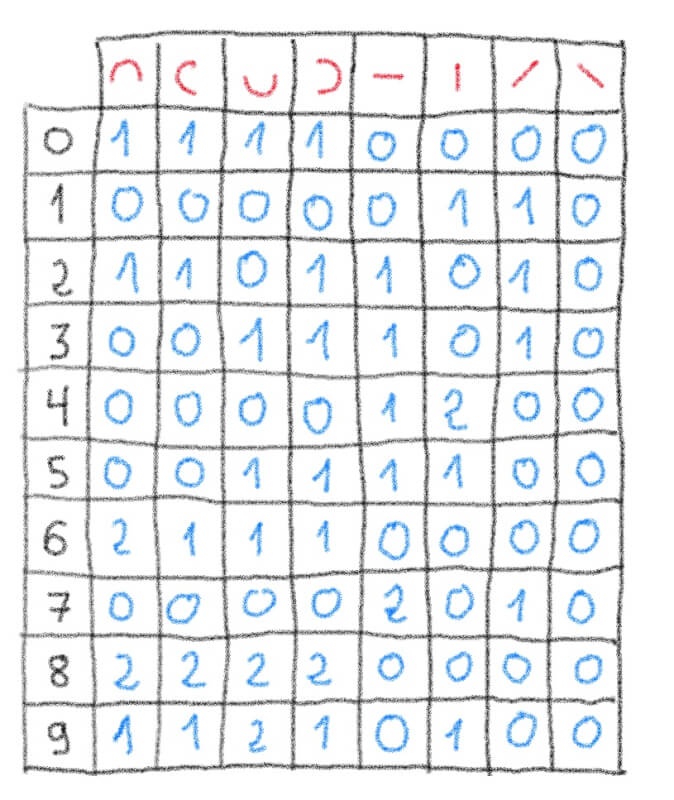
Теперь давайте попробуем распознать (вывести) новую рукописную цифру, подсчитав количество совпадений с одинаковыми красными формами. Затем мы сравним это с нашей предыдущей таблицей, чтобы определить, какое число имеет больше всего соответствий:
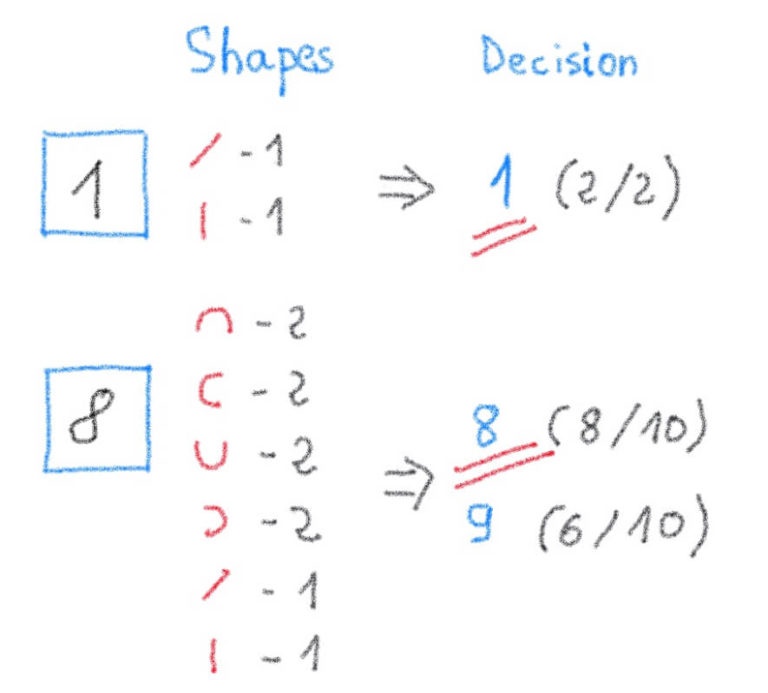
Поздравляю! Вы только что создали простейшую в мире нейросетевую систему для распознавания рукописных цифр.
Компьютер рассматривает изображение как матрицу . Черно-белое изображение — это 2D-матрица.
Рассмотрим изображение. Чтобы не усложнять задачу, возьмем небольшое черно-белое изображение цифры 8 с квадратными размерами 28 пикселей.
Каждая ячейка матрицы представляет интенсивность пикселя от 0 (который представляет черный цвет) до 255 (который представляет чистый белый пиксель).
Таким образом, изображение будет представлено в виде следующей матрицы 28 x 28 пикселей.
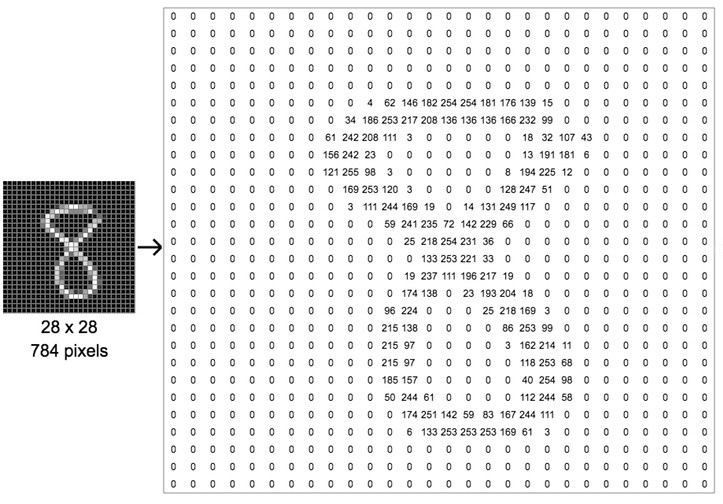
Чтобы выяснить, какой узор отображается на картинке (в данном случае рукописная цифра 8), мы будем использовать своего рода сигнал летучей мыши / фонарик. В машинном обучении фонарик называется фильтром. Фильтр используется для выполнения классического вычисления матрицы свертки, используемого в обычном программном обеспечении для обработки изображений, таком как Gimp.

Фильтр просканирует изображение , чтобы найти узор на изображении, и вызовет положительную обратную связь, если будет найдено совпадение. Это немного похоже на коробку сортировки формы малыша: треугольный фильтр соответствует треугольному отверстию, квадратный фильтр соответствует квадратному отверстию и так далее.

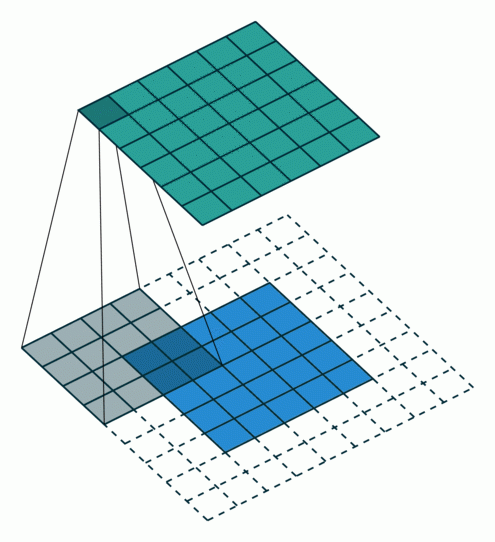
Чтобы быть более научным, процесс фильтрации изображений немного похож на анимацию ниже. Как видите, каждый шаг сканирования фильтра независим , а это значит, что эту задачу можно сильно распараллелить .
Важно отметить, что десятки фильтров будут применяться одновременно, параллельно, поскольку ни один из них не является зависимым.
Мы только что видели, что входное изображение / матрица фильтруется с использованием множественных сверток матриц.
Чтобы повысить точность распознавания изображений, просто возьмите отфильтрованное изображение из предыдущей операции и фильтруйте снова, снова и снова…
Конечно, мы несколько упрощаем, но, как правило, чем больше фильтров вы применяете и чем больше вы повторяете эту операцию последовательно, тем точнее будут ваши результаты.
Это похоже на создание новых слоев абстракции, чтобы получить более четкое и ясное описание фильтра объекта, начиная с простых фильтров и заканчивая фильтрами, которые выглядят как края, колесо, квадраты, кубы,…
Изображение стоит тысячи слов: следующее изображение представляет собой упрощенный вид исходного изображения (8 × 8), отфильтрованного с помощью фильтра свертки (3 × 3). Проекция фонарика (в этом примере фильтр Sobel Gx) дает одно значение.
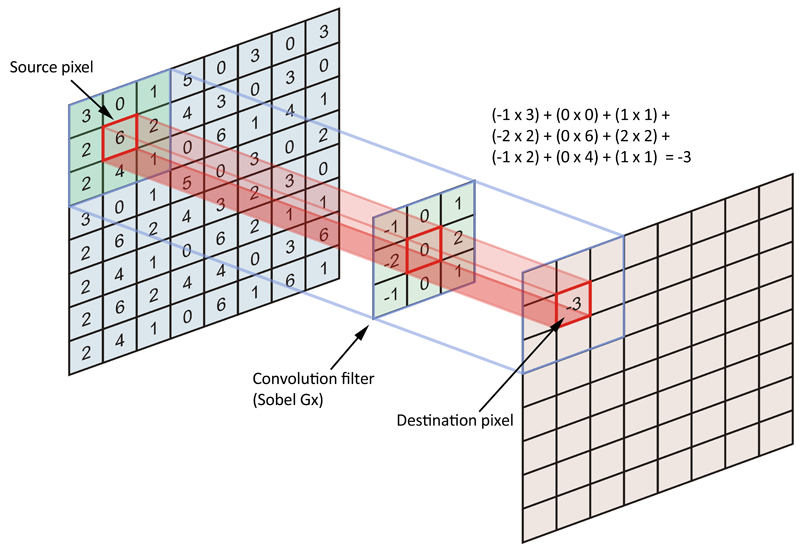
Пример фильтра свертки (Sobel Gx), примененного к входной матрице (Источник: datascience.stackexchange.com/questions/23183/why-convolutions-always-use-odd-numbers-as-filter-size/23186)
Именно здесь происходит чудо: простые матричные операции сильно распараллелены, что идеально подходит для случая использования универсального графического процессора.
Нам нужно обобщить то, что было обнаружено фильтрами, чтобы обобщить знания .
Для этого мы возьмем образец вывода предыдущей операции фильтрации.
Эта операция представляет собой объединение вызовов или понижающую дискретизацию, но на самом деле речь идет об уменьшении размера матрицы.
Вы можете использовать любую операцию уменьшения, такую как: max, min, average, count, median, sum и т. Д.
Давайте не будем забывать о главной цели нейронной сети, над которой мы работаем: построение системы распознавания изображений, также называемой классификацией изображений .
Если целью нейронной сети является обнаружение рукописных цифр, в конце будет 10 классов для сопоставления входного изображения с: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Чтобы сопоставить этот ввод с классом после прохождения всех этих фильтров и слоев понижающей дискретизации, у нас будет всего 10 нейронов (каждый из которых представляет класс), и каждый будет подключаться к последнему подвыборочному слою.
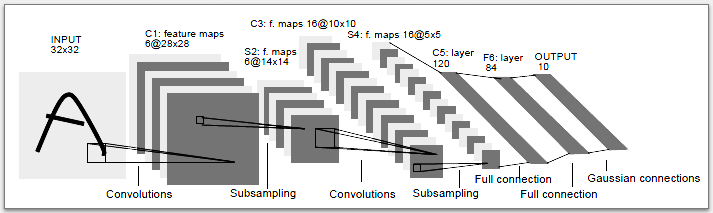
Ниже приведен обзор оригинальной сверточной нейронной сети LeNet-5, разработанной Яном Лекуном, одним из немногих, кто начал использовать эту технологию для распознавания изображений.
Красота технологии заключается не только в свертке, но и в способности сети учиться и адаптироваться сама по себе. Реализуя цикл обратной связи, называемый обратным распространением, сеть будет смягчать и подавлять некоторые «нейроны» на разных уровнях, используя веса .
Давайте KISS (будьте проще): мы смотрим на выход сети, если предположение (выход 0,1,2,3,4,5,6,7,8 или 9) неверно, мы смотрим, какой фильтр (ы) «сделал ошибку», мы присваиваем этому фильтру или фильтрам небольшой вес, чтобы они не повторили ту же ошибку в следующий раз. И вуаля! Система учится и продолжает совершенствоваться.
Обработка тысяч изображений, запуск десятков фильтров, применение понижающей дискретизации, сглаживание вывода… все эти шаги могут выполняться параллельно, что делает систему невероятно параллельной . Как ни странно, на самом деле это совершенно параллельная проблема, и это просто идеальный вариант использования GPGPU (General Purpose Graphic Processing Unit), которые идеально подходят для массовых параллельных вычислений.
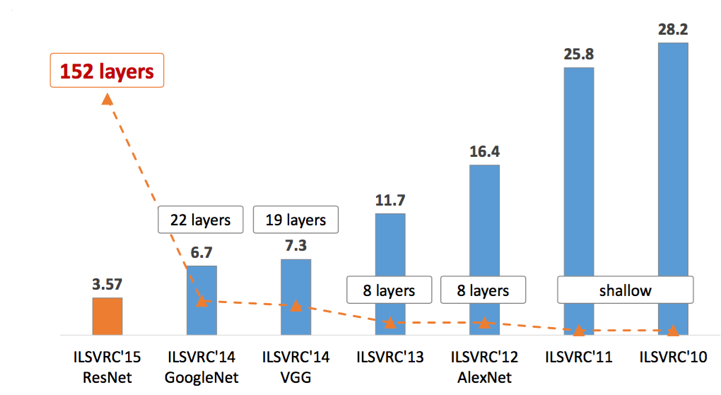
Конечно, это немного упрощение, но если мы посмотрим на основное «соревнование по распознаванию изображений», известное как задача ImageNet, мы увидим, что частота ошибок уменьшалась с увеличением глубины нейронной сети. Общепризнано, что, помимо других элементов, глубина сети приведет к большей способности к обобщению и точности.
Мы кратко рассмотрели концепцию глубокого обучения применительно к распознаванию изображений. Стоит отметить, что почти каждая новая архитектура для распознавания изображений (медицинская, спутниковая, автономное вождение и т. Д.) Использует одни и те же принципы с разным количеством слоев, разными типами фильтров, разными точками инициализации, разными размерами матриц, разными уловками (например, с изображением увеличение, дропауты, сжатие веса,…). Концепции остались прежними:
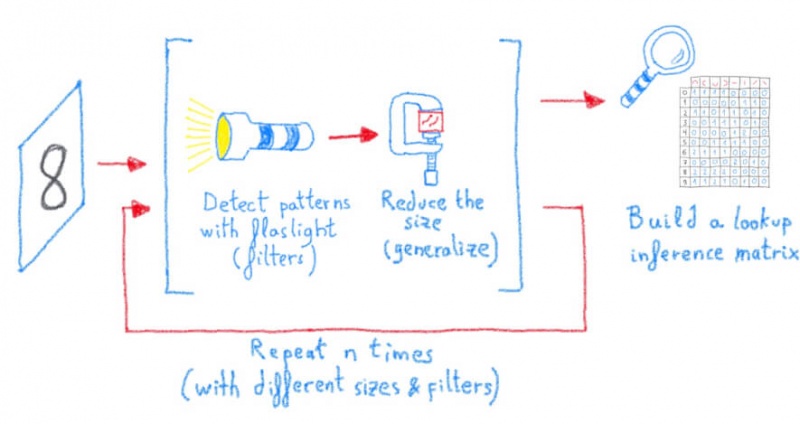
Другими словами, мы увидели, что обучение и вывод моделей глубокого обучения сводится к множеству базовых матричных операций, которые можно выполнять параллельно, и это именно то, для чего созданы наши старые добрые графические процессоры (GPU).
В следующем посте мы обсудим, как именно работает графический процессор и как технически в нем реализовано глубокое обучение.

Однако это не новые концепции. Первая искусственная нейронная сеть (ИНС) была представлена в 40-х годах. Так почему же в последнее время такой интерес к нейронным сетям и глубокому обучению?
Мы рассмотрим эту и другие концепции в серии сообщений блога о графических процессорах и машинном обучении .
YABAIR — еще один блог о распознавании изображений
Я помню, как в 80-е мой отец создавал распознавание символов для банковских чеков. Он использовал примитивы и производные для определения уровня темноты пикселей. Изучение стольких разных типов почерка было настоящей болью, потому что ему требовалось одно уравнение, применимое ко всем вариантам.
В последние несколько лет стало ясно, что лучший способ справиться с подобными проблемами — это сверточные нейронные сети. Уравнения, разработанные людьми, больше не подходят для обработки бесконечных почерков.
Давайте рассмотрим один из самых классических примеров: построение системы распознавания чисел, нейронной сети для распознавания рукописных цифр.
Факт 1: это так же просто, как подсчет
Мы начнем с подсчета, сколько раз маленькие красные фигурки в верхнем ряду можно увидеть на каждой из черных рукописных цифр (в левом столбце).

Теперь давайте попробуем распознать (вывести) новую рукописную цифру, подсчитав количество совпадений с одинаковыми красными формами. Затем мы сравним это с нашей предыдущей таблицей, чтобы определить, какое число имеет больше всего соответствий:

Поздравляю! Вы только что создали простейшую в мире нейросетевую систему для распознавания рукописных цифр.
Факт 2: изображение — это просто матрица
Компьютер рассматривает изображение как матрицу . Черно-белое изображение — это 2D-матрица.
Рассмотрим изображение. Чтобы не усложнять задачу, возьмем небольшое черно-белое изображение цифры 8 с квадратными размерами 28 пикселей.
Каждая ячейка матрицы представляет интенсивность пикселя от 0 (который представляет черный цвет) до 255 (который представляет чистый белый пиксель).
Таким образом, изображение будет представлено в виде следующей матрицы 28 x 28 пикселей.

Факт 3: сверточные слои — это просто сигналы летучей мыши
Чтобы выяснить, какой узор отображается на картинке (в данном случае рукописная цифра 8), мы будем использовать своего рода сигнал летучей мыши / фонарик. В машинном обучении фонарик называется фильтром. Фильтр используется для выполнения классического вычисления матрицы свертки, используемого в обычном программном обеспечении для обработки изображений, таком как Gimp.

Фильтр просканирует изображение , чтобы найти узор на изображении, и вызовет положительную обратную связь, если будет найдено совпадение. Это немного похоже на коробку сортировки формы малыша: треугольный фильтр соответствует треугольному отверстию, квадратный фильтр соответствует квадратному отверстию и так далее.

Факт 4: сопоставление фильтров — это досадно параллельная задача.
Чтобы быть более научным, процесс фильтрации изображений немного похож на анимацию ниже. Как видите, каждый шаг сканирования фильтра независим , а это значит, что эту задачу можно сильно распараллелить .
Важно отметить, что десятки фильтров будут применяться одновременно, параллельно, поскольку ни один из них не является зависимым.

Факт 5: просто повторите операцию фильтрации (свертку матрицы) как можно больше раз.
Мы только что видели, что входное изображение / матрица фильтруется с использованием множественных сверток матриц.
Чтобы повысить точность распознавания изображений, просто возьмите отфильтрованное изображение из предыдущей операции и фильтруйте снова, снова и снова…
Конечно, мы несколько упрощаем, но, как правило, чем больше фильтров вы применяете и чем больше вы повторяете эту операцию последовательно, тем точнее будут ваши результаты.
Это похоже на создание новых слоев абстракции, чтобы получить более четкое и ясное описание фильтра объекта, начиная с простых фильтров и заканчивая фильтрами, которые выглядят как края, колесо, квадраты, кубы,…
Факт 6: свертки матрицы — это просто x и +
Изображение стоит тысячи слов: следующее изображение представляет собой упрощенный вид исходного изображения (8 × 8), отфильтрованного с помощью фильтра свертки (3 × 3). Проекция фонарика (в этом примере фильтр Sobel Gx) дает одно значение.

Пример фильтра свертки (Sobel Gx), примененного к входной матрице (Источник: datascience.stackexchange.com/questions/23183/why-convolutions-always-use-odd-numbers-as-filter-size/23186)
Именно здесь происходит чудо: простые матричные операции сильно распараллелены, что идеально подходит для случая использования универсального графического процессора.
Факт 7. Необходимо упростить и обобщить то, что было обнаружено? Просто используйте max ()
Нам нужно обобщить то, что было обнаружено фильтрами, чтобы обобщить знания .
Для этого мы возьмем образец вывода предыдущей операции фильтрации.
Эта операция представляет собой объединение вызовов или понижающую дискретизацию, но на самом деле речь идет об уменьшении размера матрицы.
Вы можете использовать любую операцию уменьшения, такую как: max, min, average, count, median, sum и т. Д.
Факт 8: сожмите все, чтобы встать на ноги
Давайте не будем забывать о главной цели нейронной сети, над которой мы работаем: построение системы распознавания изображений, также называемой классификацией изображений .
Если целью нейронной сети является обнаружение рукописных цифр, в конце будет 10 классов для сопоставления входного изображения с: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Чтобы сопоставить этот ввод с классом после прохождения всех этих фильтров и слоев понижающей дискретизации, у нас будет всего 10 нейронов (каждый из которых представляет класс), и каждый будет подключаться к последнему подвыборочному слою.
Ниже приведен обзор оригинальной сверточной нейронной сети LeNet-5, разработанной Яном Лекуном, одним из немногих, кто начал использовать эту технологию для распознавания изображений.

Факт 9: Глубокое обучение — это просто Бережливое производство — постоянное улучшение на основе обратной связи
Красота технологии заключается не только в свертке, но и в способности сети учиться и адаптироваться сама по себе. Реализуя цикл обратной связи, называемый обратным распространением, сеть будет смягчать и подавлять некоторые «нейроны» на разных уровнях, используя веса .
Давайте KISS (будьте проще): мы смотрим на выход сети, если предположение (выход 0,1,2,3,4,5,6,7,8 или 9) неверно, мы смотрим, какой фильтр (ы) «сделал ошибку», мы присваиваем этому фильтру или фильтрам небольшой вес, чтобы они не повторили ту же ошибку в следующий раз. И вуаля! Система учится и продолжает совершенствоваться.
Факт 10: все сводится к тому, что глубокое обучение до неловкости параллельно
Обработка тысяч изображений, запуск десятков фильтров, применение понижающей дискретизации, сглаживание вывода… все эти шаги могут выполняться параллельно, что делает систему невероятно параллельной . Как ни странно, на самом деле это совершенно параллельная проблема, и это просто идеальный вариант использования GPGPU (General Purpose Graphic Processing Unit), которые идеально подходят для массовых параллельных вычислений.
Факт 11: нужно больше точности? Просто иди глубже
Конечно, это немного упрощение, но если мы посмотрим на основное «соревнование по распознаванию изображений», известное как задача ImageNet, мы увидим, что частота ошибок уменьшалась с увеличением глубины нейронной сети. Общепризнано, что, помимо других элементов, глубина сети приведет к большей способности к обобщению и точности.

В заключение
Мы кратко рассмотрели концепцию глубокого обучения применительно к распознаванию изображений. Стоит отметить, что почти каждая новая архитектура для распознавания изображений (медицинская, спутниковая, автономное вождение и т. Д.) Использует одни и те же принципы с разным количеством слоев, разными типами фильтров, разными точками инициализации, разными размерами матриц, разными уловками (например, с изображением увеличение, дропауты, сжатие веса,…). Концепции остались прежними:

Другими словами, мы увидели, что обучение и вывод моделей глубокого обучения сводится к множеству базовых матричных операций, которые можно выполнять параллельно, и это именно то, для чего созданы наши старые добрые графические процессоры (GPU).
В следующем посте мы обсудим, как именно работает графический процессор и как технически в нем реализовано глубокое обучение.